Найважливіші досягнення Інституту фізики конденсованих систем НАН України у 2021 році

Досліджено модель плямистих колоїдів із додатковою диполь-дипольною взаємодією між центрами частинок. Раніше подібну модель було запропоновано та використано для опису полярних асоціативних рідин, таких як вода та водні розчини. Такого типу моделі також можуть бути застосовані для опису плинів колоїдних частинок із неоднорідним розподілом заряду, наприклад, для розчинів протеїнів у глобулярному стані. З метою опису цих та інших систем запропоновано відповідні багатогустинні рівняння Орнштейна-Церніке, доповнені умовами замикання типу асоціативного середньо-сферичного наближення (АССН). Використовуючи метод факторизації Бакстера та слідуючи схемі, запропонованій Блюмом, розроблено ще два наближення – експоненційне наближення та базисне АССН. Для оцінки точності запропонованої теорії проведено відповідні розрахунки на основі методів комп’ютерного моделювання для колоїдів із чотирма плямами та диполь-дипольною взаємодією. Показано, що результати, отримані за допомогою базисного АССН, найкраще узгоджуються з даними комп’ютерного моделювання (Ю.В. Калюжний, Т.М. Пацаган, чл.-кор. НАН України М.Ф. Головко).

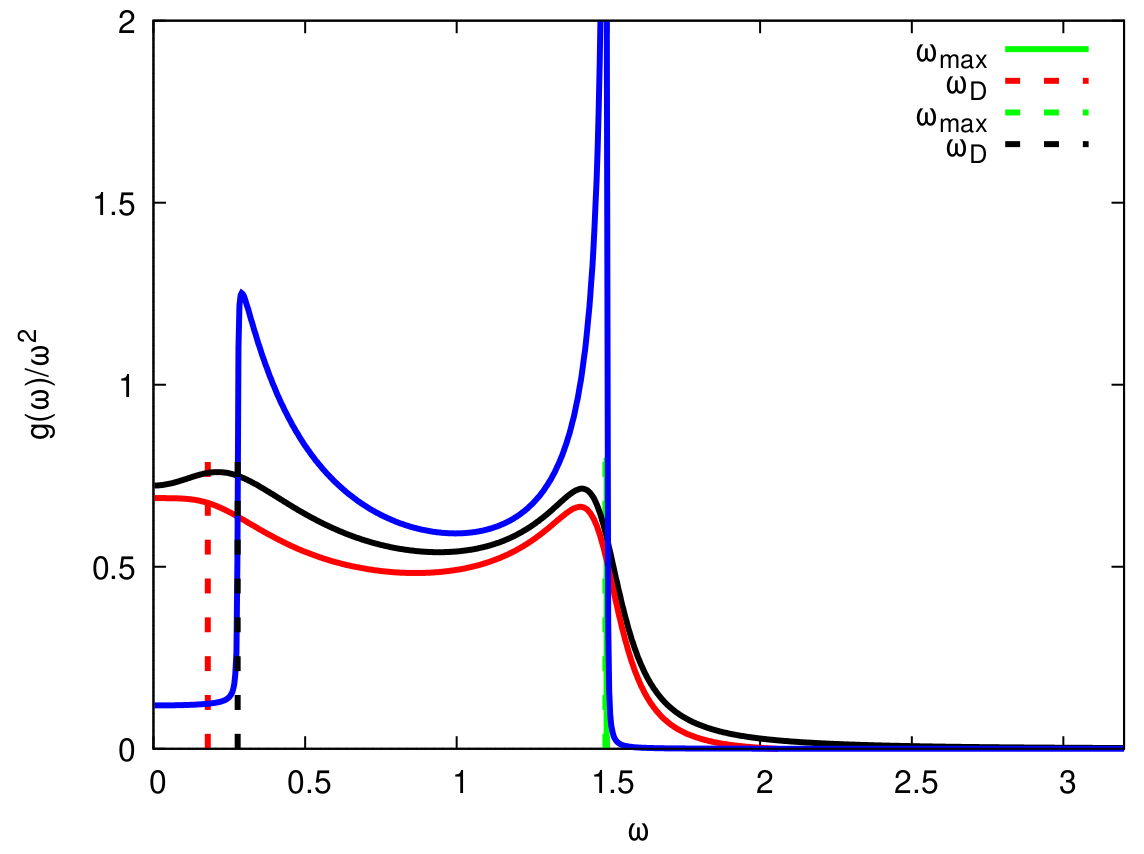
Аналіз нулів статистичної суми є одним із потужних інструментів аналізу фазових переходів і критичної поведінки. Але лише незначна частина моделей статистичної фізики дозволяє знайти координати нулів точно, для всіх інших потрібно застосовувати або наближення, або комп’ютерні симуляції. Прикладом останнього підходу є алгоритм Фукуї-Тодо для симуляції спінових систем. Перевагою цього кластерного алгоритму є те, що кожен його крок вимагає час, пропорційний до розміру системи, яку розглядають, що є суттєво краще за інші методи. Такий приріст у швидкодії досягається за рахунок того, що в рамках підходу Фукуї-Тодо немає необхідності обчислювати енергію взаємодії на кожному кроці симуляцій. І саме ця його особливість призвела до того, що стандартні методи знаходження координат нулів статистичної суми є незастосовними з алгоритмом Фукуї-Тодо. Вперше запропоновано використовувати адаптований метод перезважування для знаходження нулів статистичної суми. Цей спосіб перевірено на моделі Поттса на квадратній ґратці. Отримані в такий спосіб значення критичних параметрів добре узгоджуються як і з точними розв’язками, так і з симуляціями інших авторів. В свою чергу також показано, що, маючи навіть меншу статистику, використання нулів статистичної суми дозволяє отримати значення, які мають кращу точність, ніж отримані іншими способами (П.В. Сарканич, акад. НАН України Ю.В. Головач).

Нулі статистичної суми моделі Ізінґа на квадратній гратці розміру 48 на 48 спінів. Сині і оранжеві лінії позначають точки, де дійсна і уявна частина статистичної суми перетворюються в нуль відповідною.

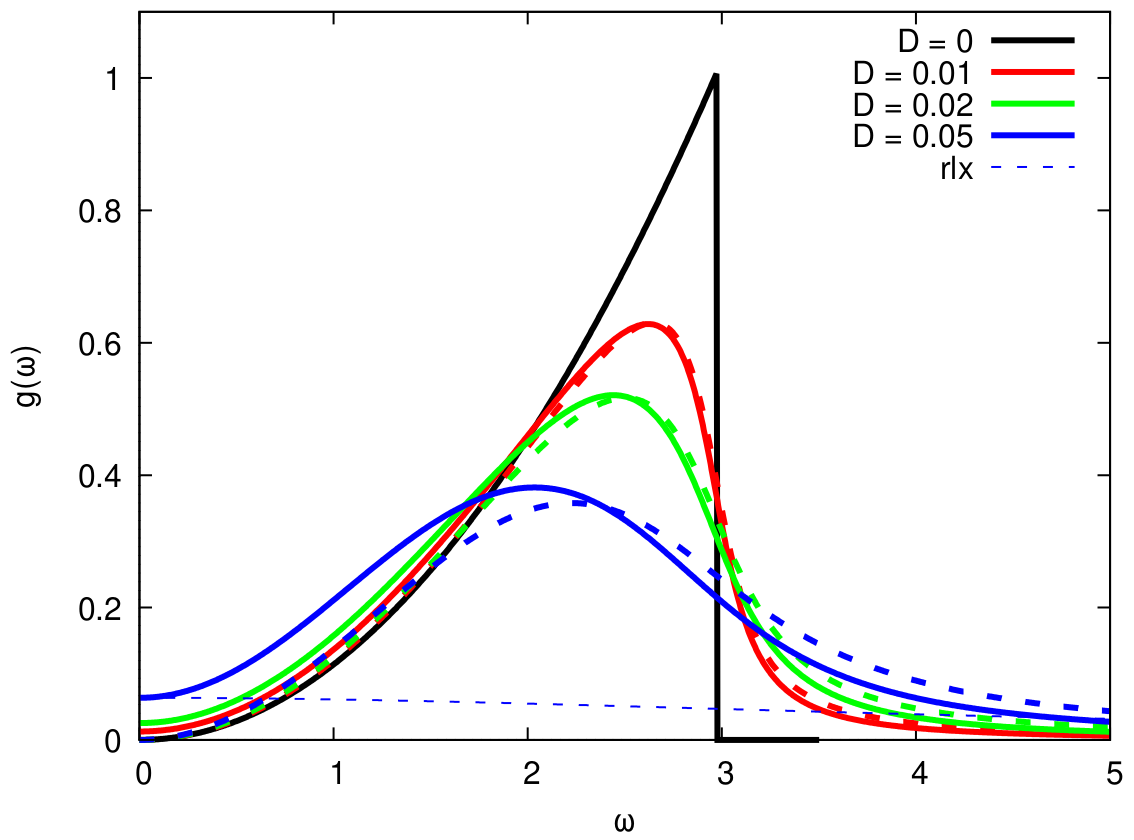
Досліджено особливості густини коливних станів для скловидних систем у рамках простої моделі акустичних мод зі згасанням Ахієзера. Отримано вираз для густини коливних станів такої моделі, який поруч із динамічним внеском дебаївського типу містить релаксаційний внесок дифузійного характеру. Розглядаються випадки як лінійної дисперсії акустичних збуджень, так і з псевдоперіодичним відхиленням від лінійності. Показано, що спостережувані особливості на коливній густині станів відповідають не бозонному піку, а сингулярностям Ван Хова, які зміщені в область низьких частот і розмиті внаслідок в’язко-дифузійної релаксації (А.М. Швайка, Т.М. Брик, М.А. Шпот).

У рамках моделі протонного впорядкування досліджено явище обертання поляризації зовнішнім електричним полем у квадратній кислоті – антисегнетоелектричному кристалі з паралельними площинами водневих зв’язків. Показано, що для електричного поля, прикладеного паралельно до цих площин, типові для антисегнетоелектриків переорієнтація поляризації підґратки та пов’язаний з цим перехід до сегнетолектричного впорядкування в квадратній кислоті відбуваються в два етапи: спершу, при певному значенні поля EII, має місце поворот поляризації однієї з підґраток на 90°, що означає фазовий перехід першого роду до неколінеарної фази з перпендикулярними поляризаціями підґраток (NC90), а лише потім, при вищих полях (EIII), після повторного повороту поляризації цієї підґратки на 90° - перехід до колінеарної сегнетоелектричної фази (FE). Побудовано φ-E фазову діаграму для низьких температур (φ – кут орієнтації зовнішнього поля) та показано, що EII ~1/cos(Δφ+π/4) і EIII~1/sin(Δφ+π/4), де Δφ – кут між електричним полем та віссю поляризації у вихідній антисегнетоелектричній фазі. Побудовані Т-E фазові діаграми для різних φ, окрім згаданих антисегнетоелектричної, неколінеарної та сегнетоелектричної фаз, також містять області з неперервним обертанням поляризації, існування яких можливе завдяки тепловим флуктуаціям, а також трикритичні точки та критичні і бікритичні кінцеві точки (А.П. Моїна).

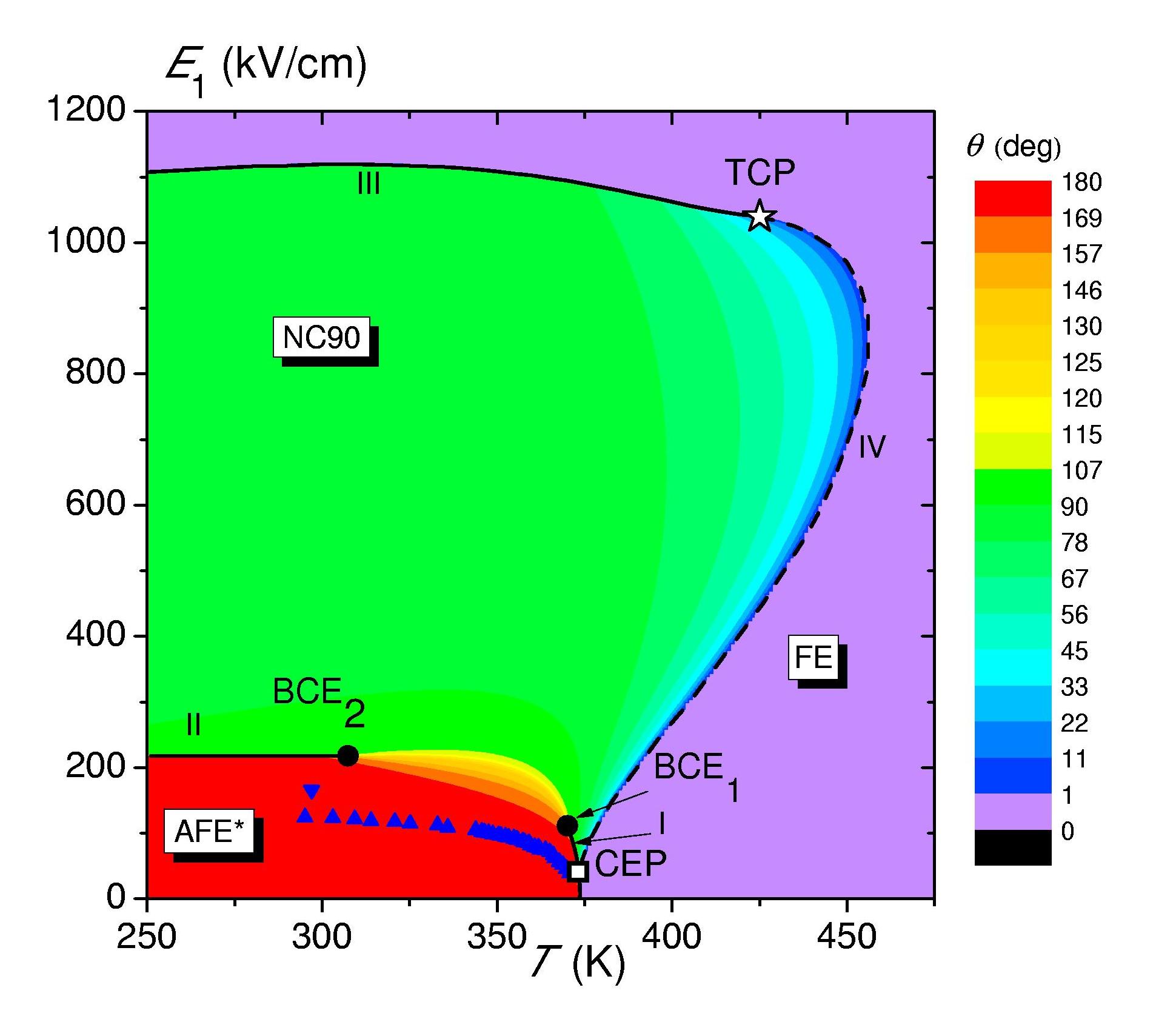
Фазова діаграма T-E1, накладена на відповідну діаграму кута між векторами поляризації підграток θ. Зазначені фази, лінії фазових переходів першого та другого родів, критичні точки та експериментальні дані.

З метою висвітлення загальних принципів, що контролюють критичну поведінку модельних рідин, досліджено як форма молекули та далекосяжність її притягальної взаємодії впливають на фазову рівновагу та критичну поведінку. Розглянуто систему твердих еліпсів із притяганням у формі квадратної ями, для якої розраховано за допомогою Монте Карло симуляцій та двох теоретичних підходів критичні параметри – температуру та густину. Встановлено, що критична температура зменшується монотонно з ростом асферичності молекули. Дану тенденцію можна успішно пояснити з точки зору сили притягання між молекулами, яку можна виміряти, зокрема, через другий віріальний коефіцієнт. Критична густина демонструє досить складну залежність від двох своїх змінних: далекосяжності притягання та асферичності молекули. Знайдено, що властивості частинкових кластерів, утворених в надкритичних станах, близьких до критичної точки, відтворюють найважливіші функціональні особливості критичної густини, включаючи кількість мінімумів та максимумів. Зокрема, показано, що модель, базована на ступені перекриття між притягальними шарами еліпсів, може якісно вірно описати зміни, спостережувані у розмірі кластерів, а також у критичній густині. На підставі отриманих результатів зроблено висновки стосовно впливу форми притягального потенціалу на критичну густину (Р.С. Мельник, Ю.В. Калюжний, А.Б. Баумкетнер).

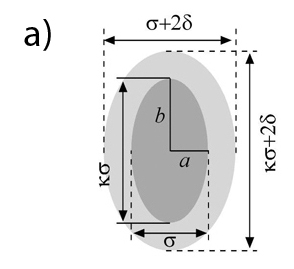
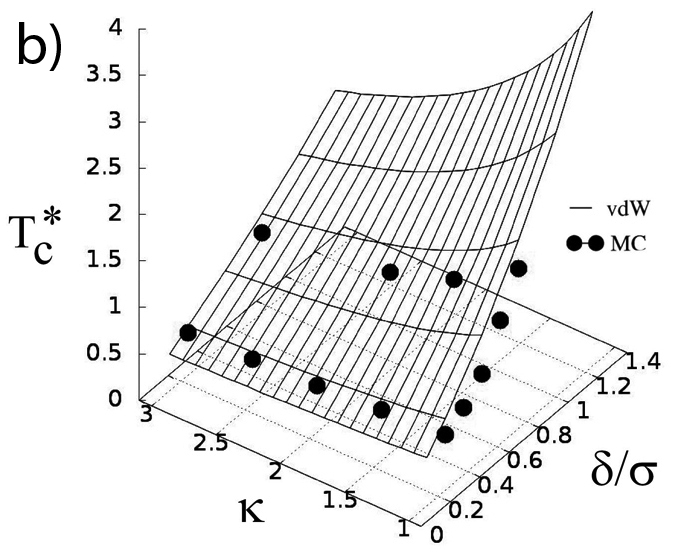
а) Модель твердого еліпсу з притяганням. Частинки взаємодіють лише коли їхні зовнішні оболонки – позначені світлим сірим кольором, перетинаються. b) Критична температура отримана як функція асферичності еліпсу κ та товщини притягального шару δ с) Критична густина як функція тих самих змінних. Дані комп’ютерних симуляцій показані разом з результатами теоретичних підходів.

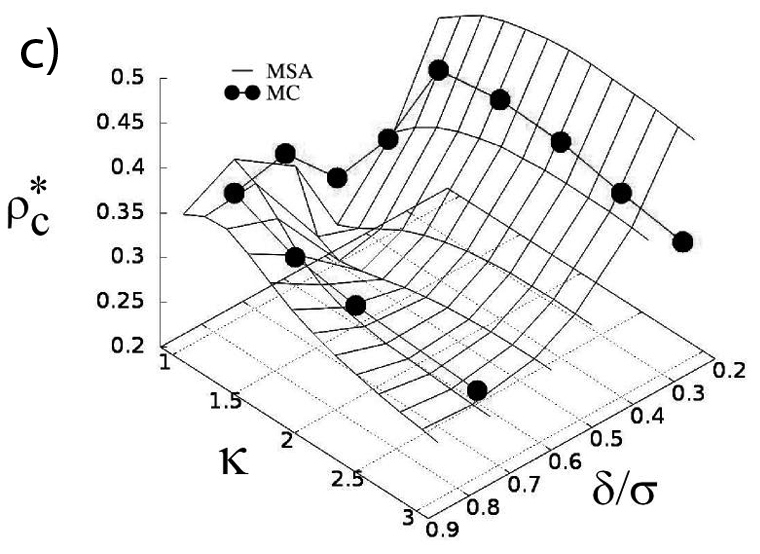
Внаслідок комплексного теоретичного та експериментального аналізу раманівських спектрів нанокомпозитного матеріалу SiO2+KH2PO4 та моделювання динаміки ґратки кристалу KH2PO4 показано, що нанокристалики KH2PO4, впроваджені у пори діаметром 10-12 нм пористої матриці SiO2, зберігають кристалічну структуру, властиву макроскопічним об’ємним кристалам KH2PO4. Вплив ефекту просторового стиснення є відносно незначним і виявляється лише у незначних механічних деформаціях нанокристаликів KH2PO4, які суттєво не змінюють симетрію кристалу KH2PO4. Як видно з рисунка (b), раманівський спектр нанокомпозиту KH2PO4+SiO2 в основних рисах відтворює спектр макроскопічного об'ємного монокристалу KH2PO4 (рисунок (с)) (Я.Й. Щур).

Досліджено рівноважні властивості адсорбату, утвореного в ході реакцій A + B →⊘ на підкладці з каталітичними елементами, розподіленими неоднорідно. Двовимірна підкладка моделюється ґраткою Бете з розподіленими випадково каталітичними зв’язками з концентрацією p. Для симетричного випадку з рівними хімічними потенціалами частинок обох сортів (μA = μB = μ) та однаковою взаємодією частинок одного й того ж сорту (JA = JB = J) точно розраховано фазову діаграму. Показано існування декількох фаз у залежності від J, μ i p: фаза зі спонтанно порушеною симетрією між частинками різних сортів, в якій вони присутні з різними середніми густинами; симетрична фаза, в якій частинки присутні при однакових густинах, а переходи між цими фазами можуть бути як першого роду, так і другого. Також існують дві додаткові фази зі структурним впорядкуванням, як наслідок розділення ґратки на дві підґратки: одна з них – це фаза, в якій частинки обох сортів з’являються переважно на одній і тій же підґратці, залишаючи другу майже порожньою, у той час як у другій фазі частинки одного сорту займають переважно одну підґратку, а частинки іншого сорту з’являються переважно на другій (Д.Ю. Шаповал, М.Л. Дудка).

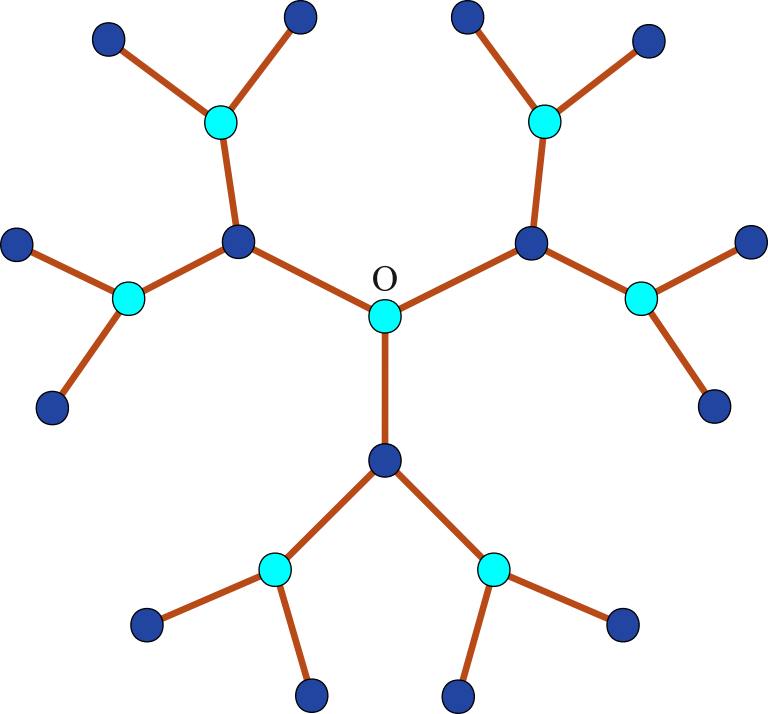
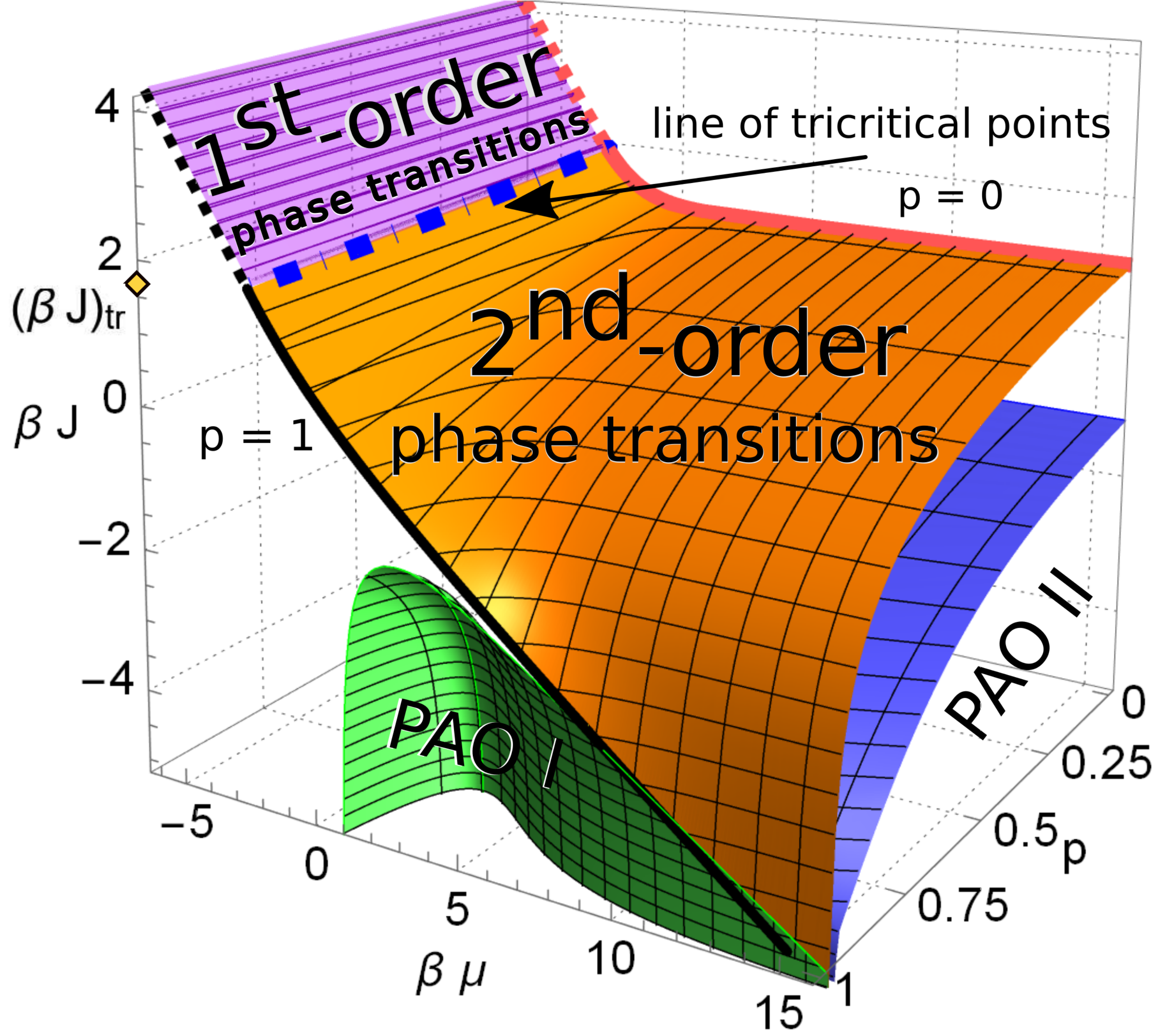
Ґратка Бете з координаційним числом q = 3 (а) та відповідна фазова діаграма двокомпонентного адсорбату (б), що складається з декількох фаз: фаза з порушеною симетрією (над поверхнями), симетрична фаза (під поверхнею), та фази з чергуючим порядком (PAO I та PAO II).

Досліджено перенормовну класичну електродинаміку в шестивимірному просторі Мінковського, яка описує заряджену частинку з жорсткістю, що є першим наближенням струни Намбу-Гото. Серед розв’язків рівняння масової оболонки вільного заряду є нелінійні коливання, що параметризуються еліптичними функціями Якобі. Рух заряду в зовнішньому електромагнітному полі описується нелінійним рівнянням з вищими похідними. Розв’язано задачу про власні вектори та власні значення тензора напруженостей електромагнітного поля, знайдено його інваріанти. Розроблено схему класифікації полів у шести вимірах, основану на цих інваріантах. Знайдено частковий розв’язок нелінійного рівняння руху заряду в зовнішньому сталому електромагнітному полі, світова лінія якого є комбінацією гіперболічної та двох колових орбіт, що лежать у трьох взаємно ортогональних площинах. Доведено його стійкість. Два додаткових виміри компактифіковано за допомогою проекції теорії на чотиривимірний простір де-Сіттера. Показано, що спіни елементарних частинок є проявом додаткових вимірів (Ю.Г. Яремко).

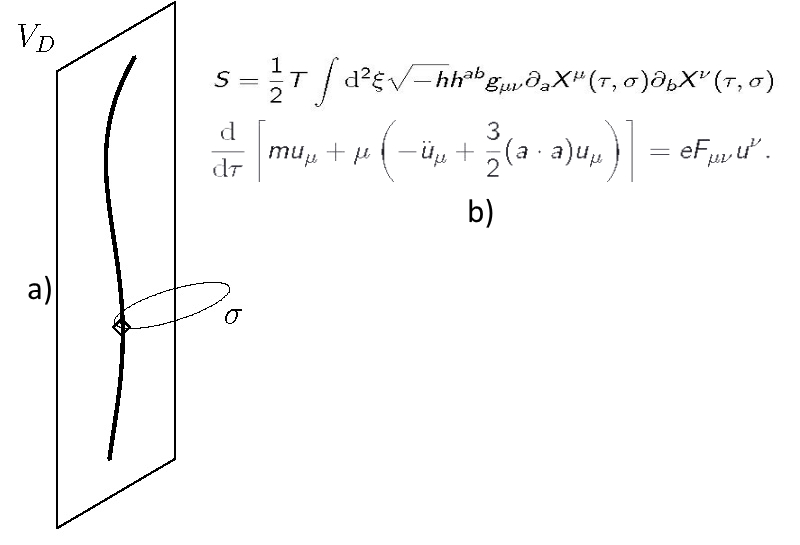
(a) Схематичне представлення зарядженої частинки у виді струни. (b) Перенормовна класична електродинаміка у 6D, яка описує заряджену частинку з жорсткістю, яка є першим наближенням струни Намбу-Гото (T – натяг струни, gμν – метрика многовиду, hab – метрика стрічки, ξ=(τ,ϭ)) та нелінійне рівняння для опису руху заряду в електромагнітному полі.

Досліджено фізичну природу та можливість розширення застосування відомого критерію Переса-Городецьких роздільності квантових станів із довільного статистичного ансамблю двох спінів 1/2 на випадок довільних статистичних ансамблів квантових систем із багатьма власними станами (тобто на випадок матриць густини ансамблю довільної розмірності). На цій основі вперше отримано низку важливих каузальних співвідношень, які обумовлюють заплутаність або, навпаки, взаємну незалежність (сепарабельність) квантових підсистем у конкретному статистичному ансамблі з відомою матрицею густини. Таким чином, вперше розроблено та отримано якісно новий “каузальний” критерій квантового заплутування (або, навпаки, сепарабельності) для квантових станів, які описуються довільними матрицями густини розмірності DN, що відповідають випадку N-поділених квантових систем, які складаються з еквівалентних квантових підсистем з D власними станами кожна. В результаті вперше отримано відповідний критерій сепарабельності для важливого окремого випадку таких систем, коли усі N підсистем квантової системи є заплутаними однією мірою одна з одною. В цьому випадку вперше отримано критерій заплутаності/сепарабельності у вигляді нерівностей для параметра заплутаності як функції характеристик N та D квантової системи. Задача, яку таким чином було вирішено, є новим, досі не відображеним у літературі, проте фундаментально важливим аспектом теорії квантового заплутування як з фундаментальної, так і з прикладної точок зору. Зокрема, отримані результати є засадничими у вирішенні важливої проблеми визначення квантової заплутаності чи, навпаки, незалежності квантових вібраційних станів, що їх виявляє квантовий детектор за вимірюваною величиною сигналу (тунельного струму та його флуктуацій) квантового детектора (Г.О. Скоробагатько).

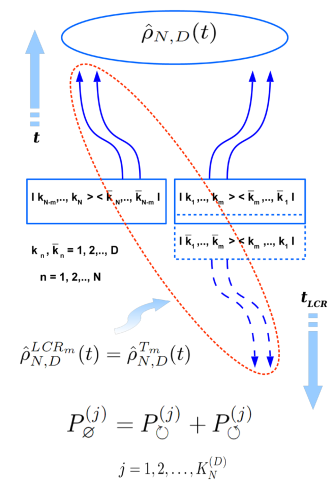
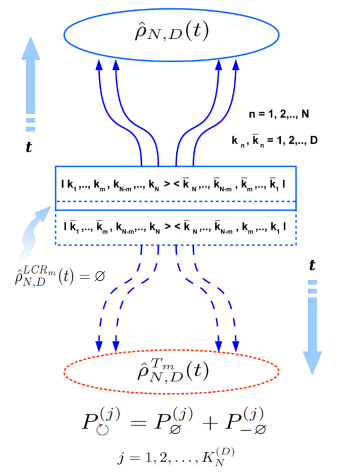
Схематичне зображення можливості локального обернення причинності для усіх сепарабельних квантових матриць густини, та неможливість такої операції для усіх тих матриць густини, які описують заплутані квантові стани усієї квантової системи (ансамблю). В першому випадку є невизначеність відносно напряму локальної еволюції сепарабельної підсистеми, а в другому – невизначеність відносно напряму глобальної стріли часу для квантово-заплутаного стану всієї квантової системи (ансамблю).

Дослідження присвячене поглибленню розуміння особливостей формування мультиферментних комплексів, яке сприятиме підвищенню ефективності гідролізу целюлози при виробництві біопалива. Поєднуючи комп’ютерне моделювання, теорію та експеримент, поставлено за мету розробити ефективні структури полімерних каркасів штучних целюлосом та знайти оптимальні сценарії їх застосування в практичних цілях. Для цього розроблено модель ферментно-полімерних комплексів різної молекулярної архітектури та, використовуючи метод комп’ютерного моделювання, досліджено процес їх самоорганізації в сумішах полімерних каркасів та вільних ферментів. Оскільки синергізм біологічних комплексів виникає внаслідок строгого порядку в розташуванні ферментів, отримані модельні комплекси проаналізовано з точки зору популяції визначених послідовностей ферментів. Встановлено, що ферментно-полімерні комплекси, адсорбовані на поверхні целюлози, призводять до відчутного росту популяції визначених послідовностей порівняно з випадком адсорбції суміші вільних ферментів. Ефект посилюється при зростанні довжини заданої послідовності і є особливо сильним для невеликої густини адсорбції, що суттєво з точки зору потенційної ефективності комплексів (Т.М. Пацаган, Я.М. Ільницький). 

Внутрішні зв’язки між концепціями певної ділянки науки відображають структуру відповідної області знання. Для того, щоб отримати якісне уявлення та кількісний опис цієї структури, здійснено емпіричний аналіз та моделювання мережі наукових концепцій фізики. Для цього використовувалися масив рукописів, зібраних у електронному репозиторії arXiv, та словник наукових концепцій, сформований за допомогою платформи ScienceWISE.info. Мережа наукових концепцій будується на основі даних про їх співпояву в документах. Результуюча мережа характеризується низкою специфічних властивостей (висока густина, дисортативність, структурні кореляції, асиметричний розподіл ступенів вузлів), які не є результатом простого процесу зростання мережі, який передбачається кількома класичними мережевими моделями. Продемонстровано, що пояснення емпірично спостережуваних властивостей може дати лише модель, що базується на одночасному врахуванні двох факторів: зростання мережі блоками та сценарію переважного приєднання (М.Б. Красницька, О.І. Мриглод, акад. НАН України Ю.В. Головач).

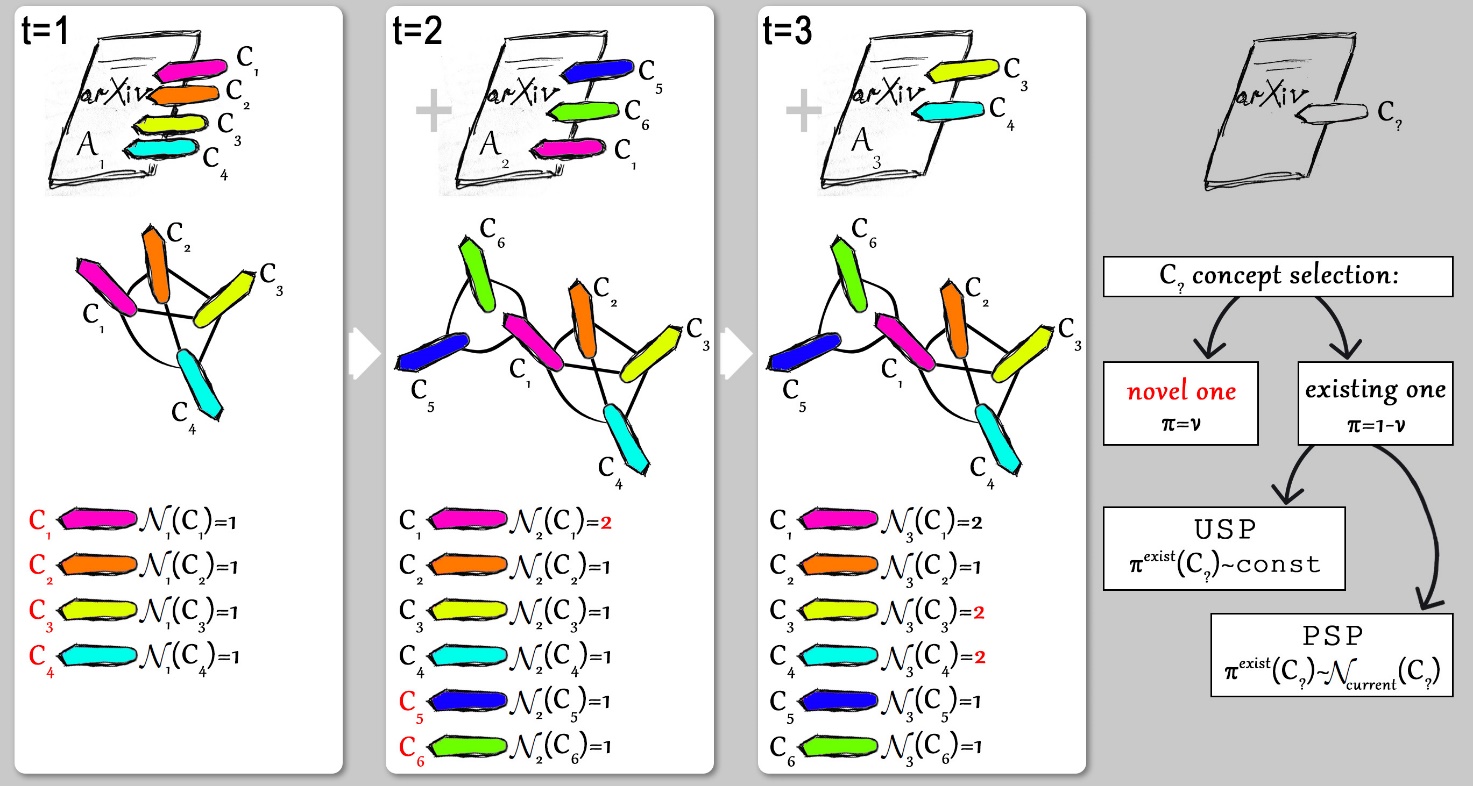
Схематична демонстрація моделі. На кожному часовому кроці t генерується нова стаття. Статті At, якій відповідає nt концепцій, входить у мережу як повний граф, впливаючи на зміну значення числа появ Nt(Ct) концепції Ci. В момент генерації нової статті At, всі її nt концепцій мають бути задані – це імовірнісний процес. Концепція Ci може виявитися або новою (такою, що в принципі з’явилася вперше саме у цій статті At) , або однією із концепцій, які були введені на попередніх кроках. При цьому можливі два сценарії того, яку із набору наявних концепцій обрати: випадковий рівномірний процес обрання (uniform selection process, USP) та процес переважного обрання (preferential selection process, PSP).