Найважливіші досягнення Інституту фізики конденсованих систем НАН України у 2024 році

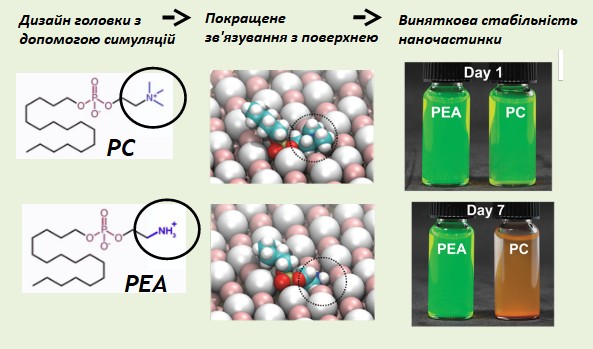
Успіх у використанні колоїдних напівпровідникових нанокристалів (НК) в оптоелектроніці невід’ємний від властивостей їх поверхні. Функціонізація НК перовскіту галогеніду свинцю є проблемною через його структурну лабільність на відміну від добре вивченого ковалентного лігандного блокування звичайних напівпровідникових НК. Обширна та нескладна молекулярна інженерія фосфоліпідів як цвіттеріонних поверхнево-активних речовин може забезпечити високоспеціалізовану хімію поверхні для галогенідів металів НК. Проведене в ІФКС моделювання молекулярної динаміки вказує, що поверхнева спорідненість ліганд-НК в основному регулюється структурою цвіттеріонної головної групи, зокрема, геометричною здатністю аніонних і катіонних частин приєднуватися до вузлів поверхневої ґратки, що підтверджується експериментально. Фосфоліпіди первинного амонію зі сумісною ґраткою підвищують структурну та колоїдну цілісність гібридних органіко-неорганічних галогенідних перовскітів свинцю (FAPbBr3 і MAPbBr3, FA – формамідиній, MA – метиламоній) і НК, що не містять свинцю. Показано, що молекулярна структура хвоста органічного ліганду визначає тривалу колоїдну стабільність і сумісність із розчинниками різної полярності. Ці НК демонструють квантовий вихід фотолюмінесценції понад 96% у розчинах та твердих матрицях (А.Б. Баумкетнер).

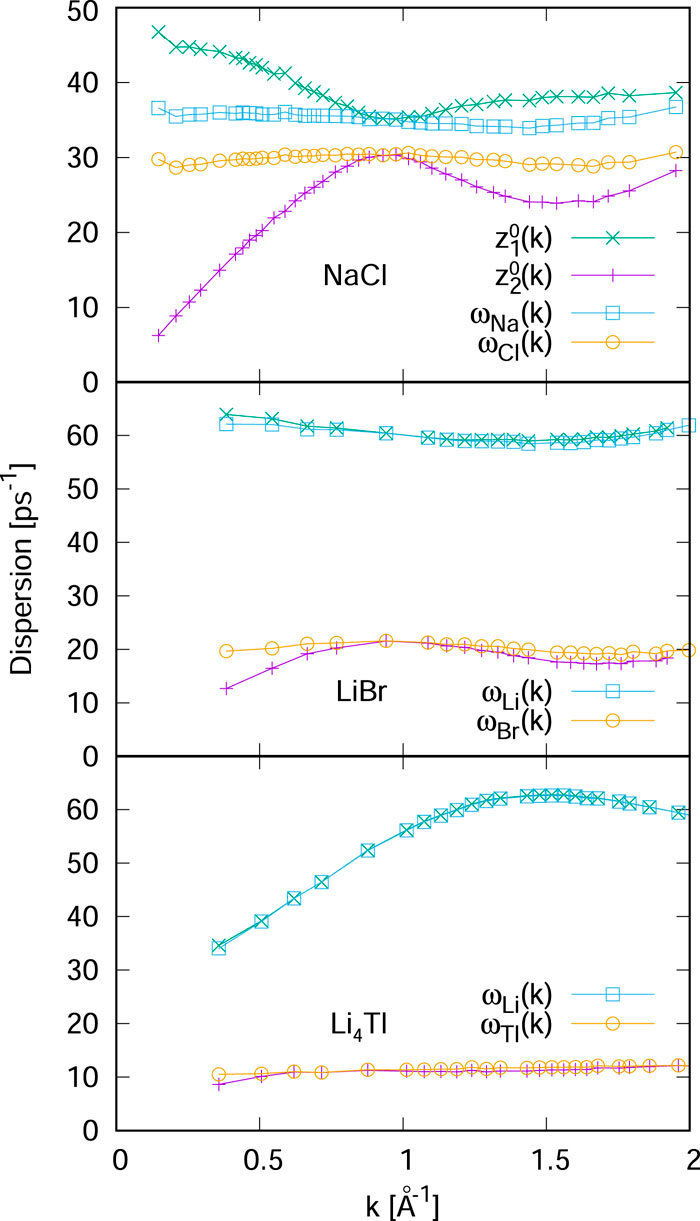
В бінарних рідинах формування спектрів колективних збуджень визначається існуванням двох гілок (акустичної та оптичної) збуджень фононного типу та взаємодією між ними. Існування так званого «швидкого звуку», який поширюється зі швидкістю в 2–3 рази вищою за макроскопічну адіабатичну швидкість, у бінарних рідинах із високою різницею мас компонент пов’язувалось із високочастотною гілкою. Загадкою було існування «швидкого звуку» в іонних розплавах із малою різницею мас компонент, зокрема в розплаві NaCl. З метою вияснення природи «швидкого звуку» в іонних розплавах проведено ab initio симуляції великої системи (2400 частинок) для розплаву NaCl та інших бінарних рідин: іонних розплавів CuCl та LiBr, металічних рідин Pb44Bi56 та Li4Tl, і звичайної ленард-джонсівської рідини KrAr. Аналіз результатів симуляцій на основі теорії узагальнених колективних мод показав, що в іонних розплавах типу NaCl далекодія відповідає за аномально велику позитивну дисперсію акустичної гілки, що відрізняється від загальноприйнятого механізму «швидкого звуку», який поширюється лише через легку компоненту бінарної рідини (чл.-кор. НАН України Т.М. Брик).

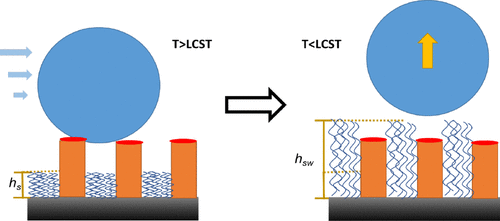
Архітектура полімерної щітки із пришпилених полімерних молекул є одним із найпоширеніших ефективних методів регулювання міжфазних взаємодій у колоїдних системах, що містяться в живих організмах та технологічних матеріалах. Нові застосування полімерних щіткових структур вимагають вирішення нових завдань щодо контролю міжфазних взаємодій. Швидкий розвиток виробництва живих клітин залежить від масштабованих і ефективних методів збору клітин. Стимул-чутливі поверхні з полі(N-ізопропілакриламіду) (PNIPAM) можуть зв’язувати та від’єднувати прикріплену клітину при зміні температури та використовуватися для росту та збору клітин. Проте їх застосування обмежені вимогою задовольняти ряд характеристик для такого покриття на основі PNIPAM, які залежать від розмірів комплексу інтегрину в клітинній мембрані та базальній поверхні. Аналіз мікроструктурованих поверхонь, коли адгезивні та роз’єднувальні функції мікродоменів роз’єднані, показує, що багатьох обмежень однокомпонентних покриттів PNIPAM можна уникнути, використовуючи набагато ширший діапазон структурних характеристик мікроструктурованих інтерфейсів, що складаються з роз’єднаних доменів PNIPAM і адгезивних полімерних доменів із клітинно-афінними функціональними групами. Контрольована температурою оборотна адгезія до таких мікроструктурованих інтерфейсів досліджена за допомогою модельних систем твердих сферичних частинок у моделюванні твердих і м’яких мембран, які взаємодіють із мікроструктурованими поверхнями, щоб імітувати взаємодію з м’якими і твердими дископодібними частинками (Д.Л. Яремчук, Я.М. Ільницький).

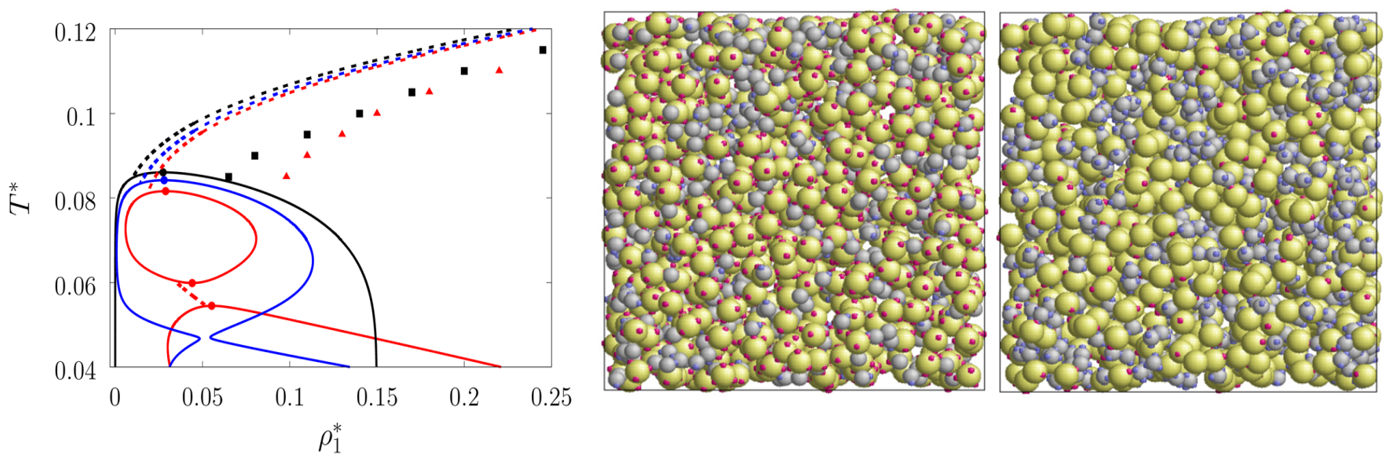
Запропоновано просту модель для функціоналізованого невпорядкованого пористого середовища і досліджено вплив такого просторового обмеження на самоасоціацію, перколяцію та фазову поведінку плину плямистих частинок. Пористе середовище моделюється у вигляді матриці випадково розподілених в об’ємі нерухомих твердих частинок сферичної форми, на поверхні яких розташовані взаємодіючі центри (плями). Плямисті частинки плину, що знаходяться у просторі, не зайнятому частинками матриці, також моделюються твердими сферами із взаємодіючими центрами на поверхні. Взаємодія між цими центрами, як на частинках плину, так і на частинках матриці, розглядається у вигляді притягального потенціалу типу квадратної ями із шириною, підібраною так, щоб дані центри могли мати лише парну взаємодію. При достатньо низьких температурах частинки, присутні в системі, можуть зв’язуватись, формуючи кластери, та, досягнувши порогу перколяції, утворювати нескінченну сітку. Фазовий перехід газ-рідина та умови виникнення явища перколяції передбачено на основі підходу, який поєднує теорію масштабної частинки для плину в пористому середовищі, термодинамічну теорію збурень Вертгайма і теорію Флорі-Стокмайєра. Показано, що запропонована теорія загалом добре узгоджується з результатами комп’ютерного моделювання. Спостережено, що ефект просторового обмеження та конкуренція між утворенням зв’язків, що з’єднують частинки плину, і зв’язками, які з’єднують частинки плину з частинками матриці, спричиняє виникнення фазової поведінки повторного входу із трьома критичними точками та двома окремими областями співіснування фаз рідини та газу (Ю.В. Калюжний, Т.М. Пацаган, чл.-кор. НАН України М.Ф. Головко).

Розробка нових лікарських засобів є складним процесом: молекула-кандидат повинна відповідати численним умовам, щоб діяти належним чином, і, водночас, спричиняти мінімум побічних ефектів. Ідеальна молекула-кандидат селективно зв’язується лише з цільовими молекулами-мішенями та не впливає на інші. Обсяг експериментальних даних про різні властивості молекул постійно зростає, що сприяє використанню підходів, заснованих на обробці даних. Застосування типових прогностичних моделей машинного навчання може суттєво ускладнитися через обмежену кількість експериментальних даних щодо певної молекули-мішені. Існує багато відомих інгібіторів тромбіну (що діють як антикоагулянти), проте кількість відомих інгібіторів білка C (коагулянтів) є надзвичайно малою. Представлено підхід для відбору нових кандидатів на роль інгібіторів шляхом побудови ефективного представлення хімічного простору. Розроблено модель глибокого навчання – автоенкодер, навчений на великому наборі молекул у форматі SMILES для відображення хімічного простору. Відпрацьовано різні стратегії генерації нових кандидатів молекул коагулянтів і випробувано запропонований підхід для пошуку молекул антикоагулянтів методами машинного навчання, де можна передбачити їхню інгібуючу дію щодо тромбіну. Проведено порівняння цього підходу з іншою генеративною моделлю глибокого навчання MegaMolBART, що використовує подібні принципи обходу хімічного простору (М.Ю. Дручок).

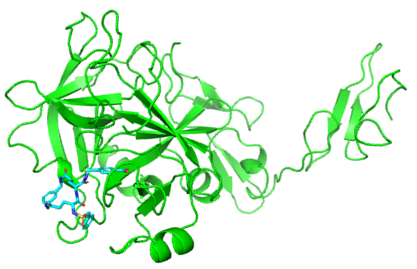
Визначення швидкості (часу адаптації), з якою біологічні системи еволюціонують, а також питання спрямованого контролю цих процесів є важливими як з теоретичної, так і з практичної точки зору (для прикладу, у процесах поширення резистентності до антибіотиків у бактерій). Досліджено роль адаптивних ландшафтів та швидкості мутації у квазівидовій моделі популяцій та застосовано деякі підходи, розвинені у статистичній фізиці, для прискорення процесів еволюції у такій моделі. Розглянуто стохастичну версію квазівидової моделі, де вводиться стохастична реплікація та смертність організмів. Кожен організм представлено бінарною послідовністю певної довжини. Внаслідок процесу реплікації і можливістю точкових мутацій, організм може продукувати нащадків із життєздатними мутаціями або летальними мутаціями. Встановлено, що присутність летальних генотипів призводить до суттєвого зменшення середнього часу адаптації популяцій, а отже, значно пришвидшує еволюційний процес. Такий же ефект досягнуто, застосовуючи методи паралельного відпалу та алгоритм Ванга-Ландау, використовуючи аналогію між температурою у спінових феромагнітних моделях та швидкістю мутації у квазівидовій моделі (В.Б. Блавацька).

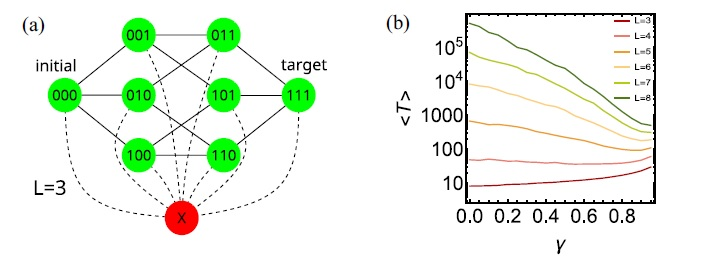
a) Схематичне зображення простору станів генотипу, представлених бінарними послідовностями довжиною L=3, лінії представляють одноточкові мутації (переходи між цими станами), червоним кольором представлено летальні стани. b) Залежність середнього часу адаптації від імовірності γ переходу у летальний стан.

У термодинамiчнiй границi поведінка спостережуваних величин поблизу точки фазового переходу над верхньою критичною вимірністю описується середньопольовою теорiєю. При цьому, скінченновимірний скейлінг, що описує псевдокритичну поведінку систем скінченного розміру, та гіперскейлінгове співвідношення, яке поєднує універсальні скейлінгові показники з вимірністю простору, порушуються. Нещодавні роботи показують, що завдяки тому, що кореляційна довжина не обмежується фізичним розміром системи, як вважалося раніше, а зростає поблизу критичної точки з більшою швидкістю, виникає нова теорія скейлінгу, задана скейлінговим показником ϙ. Цей Q-скейлінг показано у високовимірних системах із періодичними граничними умовами, зокрема за допомогою комп’ютерних симуляцій моделі Ізінґа та перколяцій. Проведено дослідження критичної поведінки у системах із вільними (відкритими) граничними умовами. Комп’ютерний експеримент кластерними методами Монте-Карло показав, що вплив поверхні на системи з малими розмірами дуже значний, що не дозволяє обчислити скейлінгові показники достатньо точно. Для цього використано аналіз нулів статистичної суми, що спирається на теорему Лі-Янґа, згідно з якою всі нулі статистичної суми системи скінченного розміру знаходяться в комплексній площині відповідних змінних. Він більш ефективний для систем малих розмірів і дозволяє побачити змістовні результати меншими обчислювальними зусиллями. Показано, що для систем з вільними граничними умовами існують два скейлінгові режими – Ґаусовий у критичній точці безмежної системи і Q-скейлінг у псевдокритичній точці для систем відповідного розміру (Ю.-І.-М.Н. Гончар, акад. НАН України Ю.В. Головач).

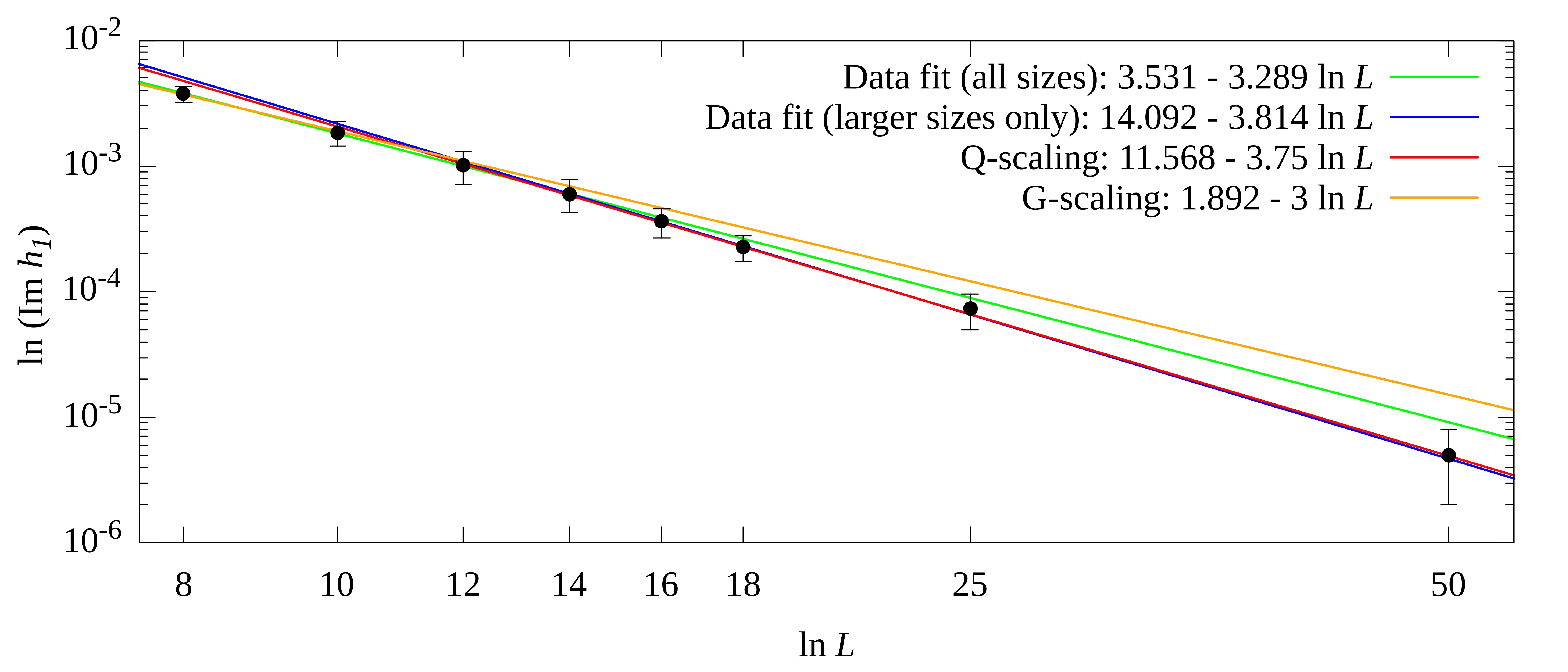
Скінченновимірний скейлінг першого нуля Лі-Янґа в комплексному зовнішньому магнітному полі для моделі Ізінґа на п’ятивимірній ґратці з вільними граничними умовами. Попри відхилення для систем малих розмірів, спостережувані в комп’ютерних симуляціях величини, позначені чорними крапками, скоро виходять на асимптотичну поведінку, ближчу до Q-скейлінгу (червона лінія – теоретичне передбачення, синя лінія – результати чисельних обчислень).

Основний стан і термодинамічні характеристики спін-1/2 дисторсного ромбічного ланцюжка Iзiнґа–Гайзенберга у магнітному полі досліджено в антиферомагнітно-феромагнітному і феромагнітно-антиферомагнітному випадках. Цей ланцюжок має точний розв’язок, що отримується за допомогою методу матриці переносу. Знайдено його основний стан на основі власних станів гамільтоніана ромбічної комірки. У випадку антиферомагнітної взаємодії Ізінґа і феромагнітної XXZ взаємодії Гайзенберга в цьому ланцюжку відсутня геометрична спінова фрустрація у класичному розумінні. Показано, що квантові флуктуації породжують ефективну геометричну фрустрацію. У випадку феромагнітної взаємодії Ізінґа і антиферомагнітної XXZ взаємодії Гайзенберга, у цьому ланцюжку є геометрична спінова фрустрація. Детально вивчено вплив квантових флуктуацій і дисторсії на основний стан, магнітні та теплові властивості моделі. Встановлено, що крива намагнічування при нульовій температурі може мати проміжні плато при нульовій намагніченості та при 1/3 намагніченості насичення. Показано, що температурна залежність питомої теплоємності у випадку антиферомагнітної взаємодії Ізінґа і феромагнітної XXZ взаємодії Гайзенберга може мати чотири максимуми при нульовому магнітному полі та п’ять максимумів при дуже слабкому магнітному полі. Походження додаткових максимумів питомої теплоємності пояснюється на основі домінуючих теплових збуджень (Б.М. Лісний).

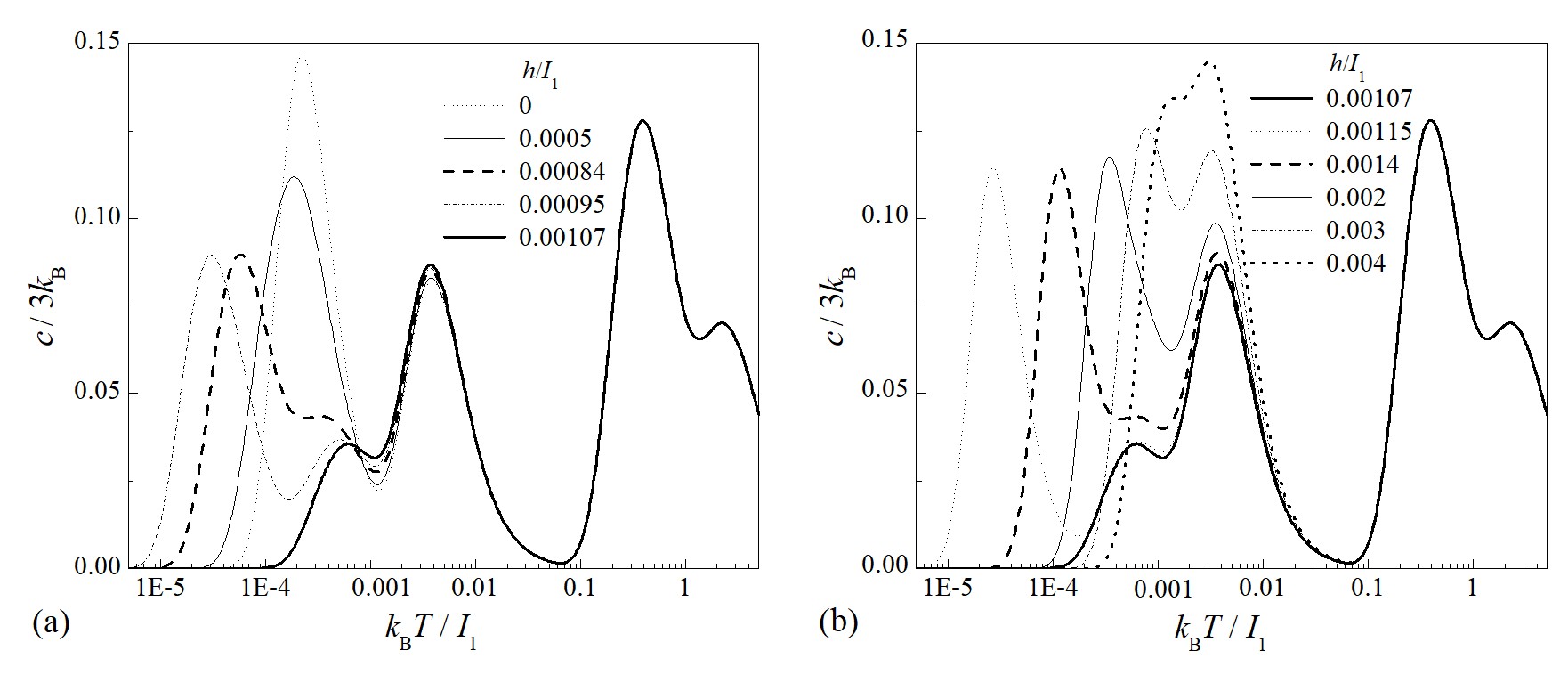
Напівлогарифмічний графік температурної залежності питомої теплоємності для феромагнітної взаємодії Гайзенберга J/I₁ = -5, Δ = 1.3, параметра дисторсії δ/I₁ = 0.4811 та кількох вибраних значень магнітного поля h/I₁.