Найважливіші досягнення Інституту фізики конденсованих систем НАН України у 2020 році

Методом першопринципного комп’ютерного моделювання встановлено особливості атомарної структури та просторового розподілу зарядової густини у водневому флюїді в області переходу від молекулярного до атомарного плину при температурі 2500 К. Аналітично показано, що довгохвильова асимптотика структурного фактора зарядової густини для чисто молекулярного водню (малі тиски) та металічного водневого плину (надвисокі тиски) повинна бути пропорційною до четвертої степені за хвильовим числом ~k⁴, що підтверджено комп’ютерним моделюванням. Однак, в області переходу від молекулярного до атомарного плину виявлено різку зміну довгохвильової асимптотики структурного фактора зарядової густини, яка виникає внаслідок сильних флуктуацій електронної густини. Це впливає на екранування протонів і, як наслідок, в структурному факторі зарядової густини в області переходу виникає внесок від іонної компоненти з довгохвильовою асимптотикою ~k². Результати першопринципного моделювання вперше дозволили обґрунтувати припущення, що в області переходу від молекулярного до атомарного плину можуть існувати не повністю заекрановані іони, що, зокрема, відображається в особливостях структури та динаміки водневого флюїду в перехідній області (Т.М. Брик).

Миттєва конфігурація молекул водню при Т=2500 К з ізоповерхнями електронної густини.

Досліджено вплив особливостей архітектури складних галужених полімерів на їх поведінку в розчині. Відомо, що особливості фолдингу окремих макромолекул і гідродинаміка полімерних розчинів суттєво залежать від характеристик розміру та форми макромолекул, що, в свою чергу, визначаються їх топологією. Використовуючи як аналітичний підхід, що базується на підході інтегрування за траєкторіями, так і чисельний підхід в рамках молекулярної динаміки, досліджено структурні властивості складних Гаусових полімерів, які містять f_c лінійних гілок та f_r замкнених петель, приєднаних до центрального кору. Для основних характеристик розміру, якими є радіус гірації R_g та гідродинамічний радіус R_H, отримано оцінки для відношення R_g/R_H в залежності від деталей полімерної архітектури. Зокрема, кількісно оцінено компактифікацію (зменшення ефективного розміру) такого складного полімерного об’єкту з ростом кількості замкнених петель f_r у порівнянні з простими молекулами такої ж сумарної молекулярної ваги. Чисельні симуляції узгоджуються з аналітичними передбаченнями і чітко демонструють зменшення відношення R_g/R_H зі збільшенням кількості петель у структурі. Отримані результати кількісно описують поведінку складних полімерів із різною архітектурою гілок у режимі Гаусового полімера (В.Б. Блавацька, Х.А. Гайдуківська).

Запропоновано модель імуноглобулінів у середовищі клітини, яке моделюється як невпорядкована пориста матриця, що формується набором твердосферних перешкод, заморожених у стані рівноваги. На основі поєднання ідей термодинамічної теорії збурень Вертхайма для асоціативних рідин, теорії масштабної частинки та теорії Флорі-Стокмайєра для полімеризації, досліджено фазову рівновагу рідина-рідина, перколяційні властивості, розподіли кластерів за розмірами та другий віріальний коефіцієнт. Показано, що для системи антитіл, які моделюються частинками У-подібної форми і поміщені в невпорядковане середовище, має місце фазова рівновага типу рідина-рідина, що залежить від сили асоціації між частинками. Встановлено, що критичні температура та густина такої моделі суттєво зменшуються, а область фазового співіснування звужується в порівнянні з об’ємним випадком. Зі збільшенням пакування частинок пористого середовища перколяційна область стає ширшою, а кількість кластерів самоасоційованих антитіл у ній зменшується, оскільки виникає нескінченний перколяційний кластер. Таким чином, пористе середовище підсилює процес кластероутворення. Інший цікавий результат дослідження – немонотонна поведінка другого віріального коефіцієнта; при низьких і середніх значеннях пакування він спершу зменшується (дестабілізація), а при вищих значеннях – зростає (Т.В. Гвоздь, Ю.В. Калюжний).

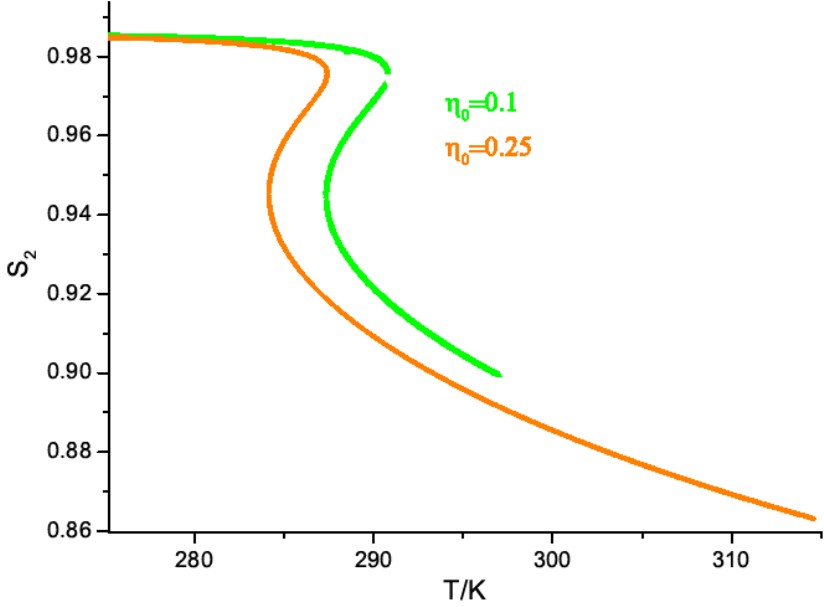
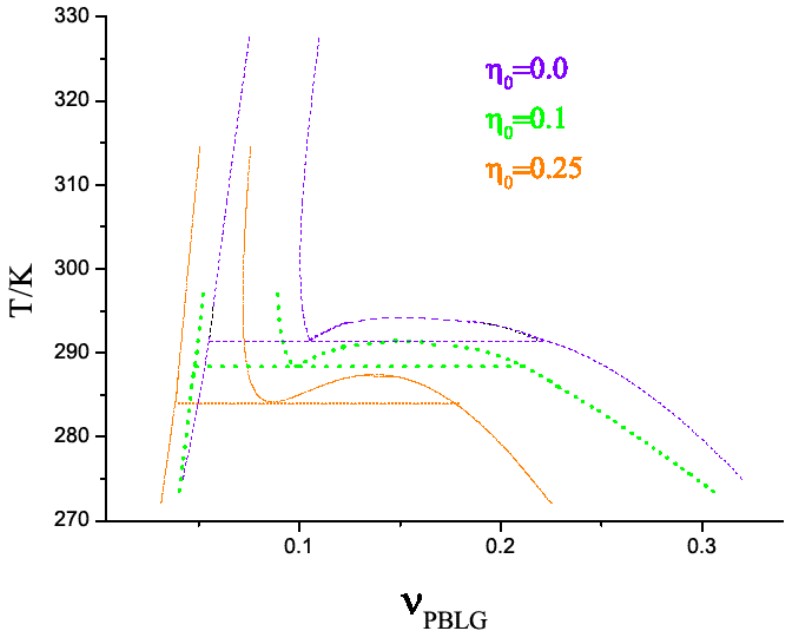
Запропоновано узагальнене рівняння Ван дер Ваальса для iзотропно-нематичної фазової рiвноваги в анiзотропних плинах у невпорядкованому пористому середовищi. Встановлено значний вплив форми мiжчастинкової притягальної взаємодiї на фазову поведінку анiзотропних плинiв. Цей ефект продемонстровано на прикладi трьох простих моделей, а саме моделi з анiзотропним притяганням Леннарда-Джонса, моделi з модифiкованим притяганням Леннарда-Джонса i моделi з анiзотропним потенцiалом квадратної ями. Запропоноване узагальнене рiвняння ван дер Ваальса використано для опису впливу пористих середовищ на фазову поведiнку розчинiв полiпептидiв у пористих середовищах. Шляхом введення температурної залежностi для глибини потенцiальної ями i геометричних параметрiв сфероцилiндра вiдтворено основнi риси фазової поведiнки полiпептиду полi (γ-бензил-L-глутамату) (PBLG) в розчинi диметилформамiду, включаючи iснування двох нематичних фаз. Показано, що наявнiсть пористого середовища зсуває фазову дiаграму в область менших густин i нижчих температур (В.І. Шмотолоха, чл.-кор. НАН України М.Ф. Головко).

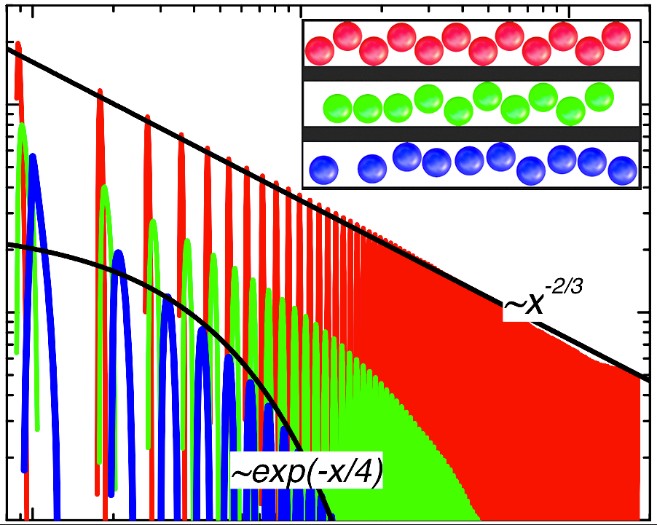
Методом комп’ютерного експерименту досліджено структурні перетворення в квазі-одномірній (q1D) системі дисків, які при щільному пакуванні відтворюють структуру, ізоморфну до зиґзаґоподібного ланцюжка у 2D трикутній ґратці при щільному пакуванні дисків. Квазіодномірність моделі забезпечується двома непроникними паралельними лініями, які формують 2D пору/канал, де знаходяться диски. При щільному пакуванні диски утворюють ідеальний зиґзаґ, коли кожен диск є закритим у комірці, утвореній стінкою та двома дисками-сусідами, оскільки щілина між ними є меншою за діаметр диску. По мірі збільшення довжини каналу (зменшення густини дисків) і послабленні просторового обмеження, тенденція до збільшення ентропії системи приводить до появи у зиґзаґоподібному кристалі локалізованих дефектів у вигляді щілин між дисками-сусідами, що стають ширшими за їхній діаметр. Це дозволяє дискам попарно вивільнятися з комірок і обмінюватися вертикальними положеннями. Показано, що згасання кореляцій у ланцюжку з дефектами відбувається за степеневим законом, що свідчить про існування у системі далекосяжного трансляційного порядку. При подальшому зменшенні густини локалізовані дефекти з’єднуються між собою і диски можуть перетинати канал незалежно. У цьому випадку кореляції згасають експоненційно, що є типово для плинів. Отримані результати демонструють, що сценарій плавлення q1D системи твердих дисків – дуже подібний до неперервного фазового переходу типу Костерліца-Таулеса у 2D системах (Т.М. Брик, А.Д. Трохимчук).

Із залученням методів конформної теорії поля (CFT) в d = 4 – ε-вимірному просторі показано, що існує однозначна відповідність між рядом Тейлора для шарової сприйнятливості (інтеграл від парної кореляційної функції за d – 1 паралельними напрямами всередині плоско-паралельного шару між відстанями z₁ і z₂ від поверхні) за степенями змінної ζ= z₁/z₂ та операторним розкладом кореляційної функції за поверхневими конформними блоками, BOE (boundary operator expansion). Ця загальна властивість не була відомою досі і дає новий інструмент для ефективних розрахунків кореляційних функцій у конформній теорії поля обмежених систем (Boundary CFT). З використанням цієї відповідності вперше розраховано з точністю до O(ε) парну кореляційну функцію при екстраординарному переході в напівбезмежних системах. Застосування рівняння бутстрапу дає об’ємний операторний розклад OPE (operator-product expansion) для кореляційної функції і усереднені скейлінгові вимірності складених (composite) скалярних операторів O(n)-моделі в порядку O(ε²), що узгоджуються з відомими результатами ε- і 1/n-розкладів (М.А. Шпот).

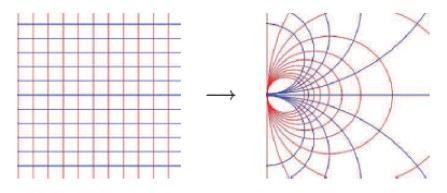
Конформні перетворення локально зберігають кути і змінюють довжини. В напівбезмежних системах зберігається поверхня. В картографії і математиці використовуються з кінця XVI сторіччя.

З допомогою першопринципного комп’ютерного моделювання досліджено еволюцію електронного спектру та оптичних властивостей при переході від однорідного монокристалічного кремнію Si до його пористого аналога з періодичною мережею пор нанорозмірного діаметру (7.34, 11.26 і 15.40 Å). Пористий Si з порами такого малого діаметру вже технологічно доступний. Досліджено вплив природніх процесів гідроксиляції поверхні пористого кварцу (впровадження груп ОН всередину пор) та проникнення молекул води з навколишнього середовища в пори на ширину забороненої зони та оптичні властивості пористого Si. Показано, що в порах найменшого діаметру 7.34 Å відбувається процес розпаду гідроксильних груп ОН та утворення незв’язаних протонів, що може бути причиною протонної провідності пористого Si. Іншими словами, пористий кремній певної морфології може змінити напівпровідникові властивості, типові для монокристалічного зразка, на властивості протонного провідника, якому відповідає рівноважна конфігурація пори кремнію, що декорована дисоційованими групами ОН, при якій утворюються вільні протони в центрі пори. Проникнення молекул води в пору руйнує протонну провідність і відновлює напівпровідникові властивості пористого Si. Показано також, що молекулярне впорядкування води та гідроксильних груп значною мірою визначає оптичні властивості (дисперсію показників заломлення та коефіцієнтів екстинкції) композитного матеріалу Si + OH + H₂O, змінюючи, для прикладу, знак оптичного двозаломлення з позитивного на негативний у широкій спектральній області ~0.2–1.0 еВ (Я.Й. Щур).

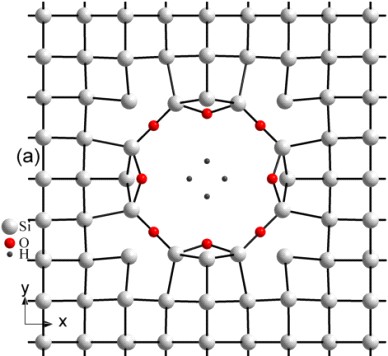
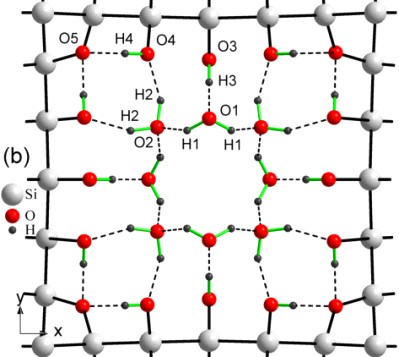
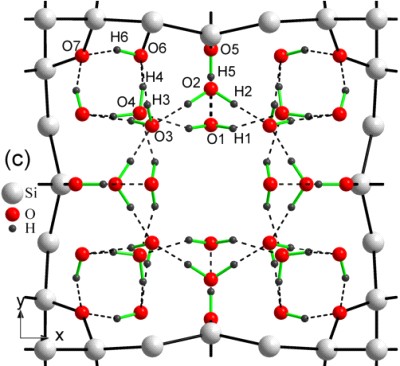
Рисунок 1. а – рівноважна конфігурація пори Si (діаметр 0.7 нм) з вільними протонами в центрі пори, отриманими в результаті дисоціації груп ОН; b, c – рівноважна конфігурація пори Si (діаметр 1.1 нм), декорованої різною кількістю гідроксильних груп та молекул води.

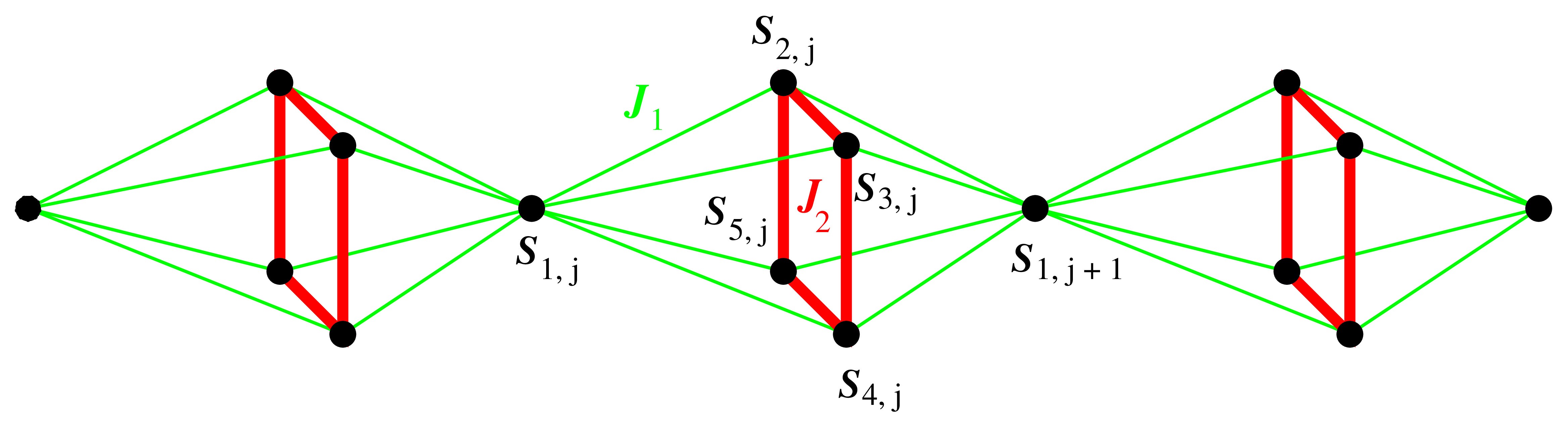
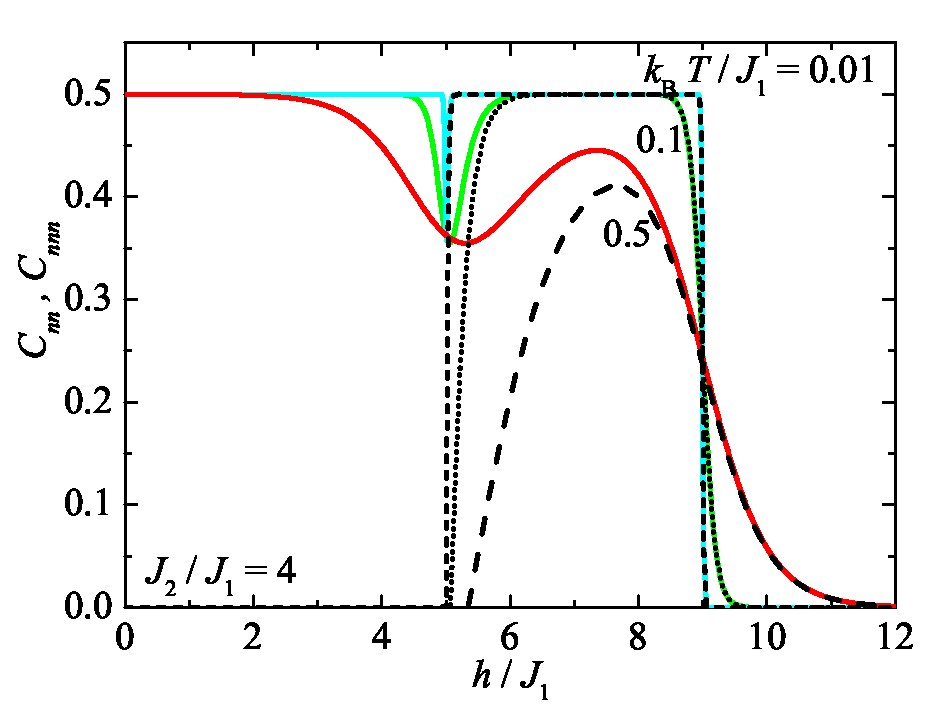
Досліджено двоспінову заплутаність між найближчими та наступними після найближчих спінами у фрустрованому спін-1/2 октаедричному ланцюжку Гайзенберга. На прикладі цієї моделі показано, що концепція локалізованих магнонів може бути адаптована до обчислення такої мiри заплутаностi, як узгодженiсть (concurrence) мiж сусiднiми та наступними пiсля сусiднiх спiнами за наявностi зовнiшнього магнiтного поля. Для перевірки результатів теорії локалізованих магнонiв застосовано метод точної діагоналізації для скінченного октаедричного ланцюжка з N = 20 вузлів. Побудовано польові залежності узгодженості між найближчими та наступними після найближчих спінами в октаедричному ланцюжку при різних температурах. Отриманi результати переконливо свідчать про можливiсть застосування концепцiї локалiзованих магнонiв для розрахунку мiри заплутаностi в широкому класi плоскозонних квантових антиферомагнетикiв Гайзенберга (О.М. Крупніцька).

Мережі співпраці – класичний приклад складних систем, що досліджуються методами складних мереж. Зокрема, відомими є типові характеристики для реальних мереж наукового співавторства, побудованих для різних ділянок науки. Проте однією з ознак сучасної науки стало формування великих стійких колаборацій науковців, які працюють у рамках проектів, що вимагають концентрації значних матеріальних і людських ресурсів. Результати їхніх досліджень публікуються за авторства колективів, що можуть включати до кількох тисяч імен. Досліджено вплив присутності таких статей на наукометричні індикатори публікаційної діяльності окремих вчених, дослідницьких центрів та усього сегменту української науки. Проведено аналіз бібліометричних даних, що отримані з наукометричної бази Scopus. Показано, що, попри незначну відносну частку публікацій за авторством великих колективів, їхній вплив на наукометричні показники може бути статистично значимим. Отримані результати свідчать про необхідність внесення змін в усталені наукометричні методики та підходи для адекватного врахування цього явища (О.І. Мриглод, акад. НАН України І.М. Мриглод).

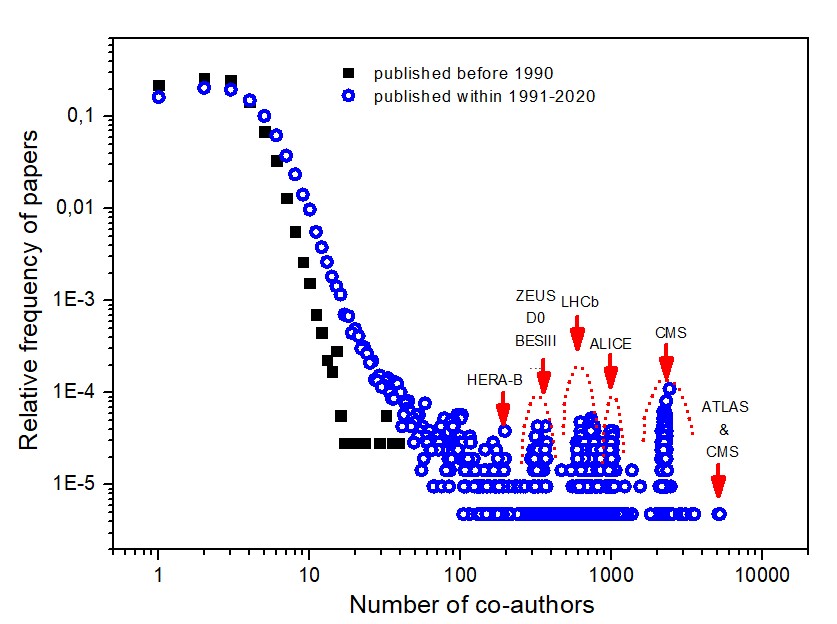
Нормалізований розподіл публікацій із БД Scopus, що мають відношення до України (на початок 2020 року), за кількістю їх авторів.